En el artículo anterior hicimos una descripción detallada del nuevo método de alineación que proponemos, y además proporcionamos la herramienta necesaria para poder ponerlo en práctica.
En este post pretendemos demostrar las bondades del procedimiento y la rapidez de ejecución. Para ello hemos desalineado completamente la montura y hemos procedido a volver a alinearla.
Las pruebas de campo que hemos realizado son las siguientes:
- Prueba 1: desalineamos la montura por completo, como si acabáramos de montar el telescopio, y realizamos una alineación rápida con el buscador de la polar. Ni siquiera nos hemos molestado en intentar ajustar especialmente bien la hora angular correspondiente (en adelante HA), sino que la acercamos ‘a ojo’ a la posición que le corresponde. En 25 minutos hemos vuelto a dejar la montura alineada con un error calculado de 9 arcseg respecto al NCP.
. - Prueba 2: desalineación total. Nos llevamos la estrella polar a un punto alejado del círculo del buscador de la polar. Es decir, no sólo no está en la HA que le corresponde, sino que además está totalmente fuera de su círculo natural de rotación. En este caso hemos tardado un poco más, unos 53 min, debido a efectos que comentamos más adelante y a que hemos repetido el procedimiento una segunda vez para dejar una alineación lo más precisa posible. El error final calculado es de 7 arcseg.
Tras este aperitivo, procedemos a explicar ambos casos con más detalle y con sus correspondientes ilustraciones.
Consideraciones previas
No es necesario volver a realizar una captura de la rotación del cielo. Tal y como explicamos en el post anterior, cuando realicemos por primera vez esta captura, podremos conservarla para siempre, y utilizarla siempre que utilicemos el mismo telescopio con el mismo tren óptico. Ni siquiera necesitamos que se trate de la misma montura.
Esto es una gran ventaja, ya que la captura del cielo rotando es la más larga (45 – 90 min.) y por tanto en próximas alineaciones nos ahorraremos tanto ese tiempo de captura como el de toma de medidas de coordenadas sobre la imagen.
Prueba 1: Partimos de una alineación básica con el buscador de la polar.
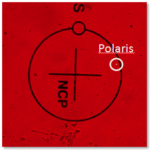
En la imagen siguiente se puede apreciar lo que se ve a través del buscador de la polar, y que constituye nuestro punto de partida
Sobre esta ilustración es interesante hacer las siguientes apreciaciones:
- No hemos ajustado la HA: no hemos utilizado el circulito sobre el cual hay que situar la polar. Lo que hemos hecho es situar la polar más o menos en la posición que le correspondería conociendo la HA.
. - No hemos situado del todo la polar sobre el círculo de rotación con el único objetivo de que se pudiera apreciar en la ilustración que mostramos. Esto introduce algo más de error, pero como veremos tiene poca importancia.
Este es nuestro punto de partida. A partir de ahora ponemos en marcha el cronómetro y contamos el tiempo que nos llevará realizar los próximos pasos hasta que hayamos finalizado la alineación.
- Paso 1: Captura de una imagen rotando manualmente la montura en RA.
Tiempo requerido: 3 minutos.
. - Paso 2: ajuste del stretching de la imagen para visualizar correctamente las estelas, y selección de 5 estelas siguiendo las indicaciones de nuestro método.
Tiempo requerido: 6-7 minutos.
. - Paso 3: Tras el paso anterior ya conocemos la desviación actual de la montura, que resulta ser de unos 3,7 minutos de arco. También conocemos la corrección que hay que aplicar, así que procedemos a alinear la montura.
Tiempo requerido: 15 minutos.
Hasta este momento hemos tardado unos 25 minutos, y me gustaría resaltar que el paso 3 nos ha llevado tanto tiempo porque los controles de azimut y altitud de nuestra EQ6 no son precisamente maravillosos, y debido a su escasa precisión hemos tenido que «perseguir» la posición final hasta que nos hemos dado por satisfechos.
Tras esta alineación hemos repetido el proceso, pero sólo para evaluar el error actual. Este proceso nos ha llevado otros 10 minutos en total (captura más cálculos). Huelga decir que esto no es necesario, pero queríamos poder aportar el error final en este post.
En resumen:
- Tiempo total de alineación tras una puesta en estación básica: 25 min.
- Tiempo extra para volver a calcular el error final: 10 min.
- Error final de la montura: 9 segundos de arco.
Si alguien consigue un resultado similar con el método de la deriva, en un solo paso y en este tiempo, le felicito (desde luego no es nuestro caso).
Prueba 2: Partimos de una desalineación muy pronunciada
Sin dar muchas explicaciones, os muestro en la siguiente imagen cómo hemos dejado el punto de partida visto a través del buscador de la polar.
A pocos de nosotros se nos ocurriría partir de una situación así, a menos que nos guste complicarnos la vida. Sin embargo eso es lo que hemos hecho para demostrar la potencia de nuestro método.
En este caso los resultados de cada paso son:
- Paso 1: Captura de la imagen RA.
Tiempo requerido: 3 minutos.
. - Paso 2: Cálculos sobre la imagen. Esta vez hemos tardado bastante más, porque al ser la desalineación tan pronunciada nos ha costado identificar las 2 primeras estrellas comunes con la imagen del cielo. Más adelante explicamos esto en detalle.
Tiempo requerido: 30 minutos.
. - Paso 3: Del paso anterior obtenemos un error actual de unos 42,4 arcmin!!
Una alineación realmente mala. Conocido el error y la corrección a aplicar nos tomamos otros 10 minutos para arreglar el desastre.
Por tanto, en esta ocasión hemos tardado unos 43 minutos en realizar todo el proceso. Y con una captura de control que hemos hecho a continuación se desprende que ahora el error es de tan solo 1,4 arcmin.
Como nos hemos vuelto exquisitos, pero sobre todo tras ver lo fácil que resulta hacer correcciones, no nos hemos conformado con esta situación, y en 10 minutos más hemos vuelto a hacer una última corrección. Esta pequeña inversión de tiempo ha supuesto alcanzar un error final de unos 7 arcseg!!!
Comentarios sobre la prueba 2
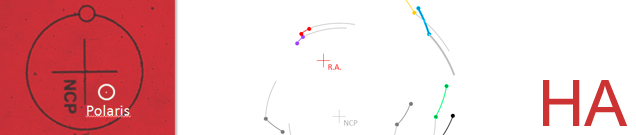
En la prueba 2 hemos comentado que la desalineación tan extrema que hemos tomado como punto de partida nos ha dificultado la identificación de estrellas comunes con la imagen del cielo inicial que ya teníamos. En la imagen que mostramos a continuación se puede entender por qué:
La imagen de la izquierda era una captura de la rotación del cielo partiendo de una puesta inicial en estación moderadamente buena, así que el centro de rotación estaba relativamente cerca del NCP.
En cambio, en la imagen de la derecha la desalineación es tal, que las estelas siguen trayectorias completamente diferentes. Nótese la separación entre ambas cruces, la de color rojo es el centro de rotación de la R.A. mientras que la de color cyan es el NCP.
Para entender el problema en toda su magnitud, sobre las mismas imágenes hemos numerado algunas estrellas comunes a ambas. Resulta evidente que es imposible guiarse por la forma de las estelas para localizar estrellas comunes.
Nosotros lo que hemos hecho es partir de una estrella que resultara obvia (en este caso Polaris) y buscar estrellas en ambas imágenes que estuvieran aproximadamente a la misma distancia (el punto de referencia es el inicio de la estela de Polaris).
Las conclusiones obvias son:
- Queda explicado por qué la prueba 2 nos ha llevado más tiempo: Ha sido complicado localizar estrellas comunes a ambas imágenes.
. - Para evitar este problema, es recomendable partir de una situación que no sea tan desastrosa como la que hemos empleado para la demostración, ya que nos hará la vida más fácil a la hora de localizar estrellas comunes entre imágenes.
. - Incluso en este caso, el método ha funcionado espectacularmente bien, así que ni siquiera esto es un obstáculo para realizar la alineación en un tiempo que opinamos que es más que razonable, y en nuestra opinión difícil de conseguir con cualquier otro método.
Por tanto y siempre que se pueda, conviene realizar una alineación previa con el buscador de la montura por el método de la hora angular. Esto nos llevará entre 5 y 10 minutos como mucho y evitará que nos encontremos en una situación como la que acabamos de describir.
Nota final para personas perspicaces 😉
Posiblemente alguno ya se habrá dado cuenta de un pequeño detalle: en realidad, si no movemos el tubo ni la cámara, el centro de rotación de la imagen RA siempre estará en las mismas coordenadas. Esto es lógico porque la posición relativa entre el telescopio y el eje de la montura se mantiene.
Por tanto, en realidad ni siquiera hubiera sido necesario volver a realizar todas las medidas de coordenadas de estelas para cada imagen R.A. que hemos capturado durante las pruebas. Simplemente nos hubiera bastado con indicar las coordenadas de las 2 primeras estelas comunes entre la imagen del cielo y la de R.A.
Sin embargo hemos preferido realizar el proceso completo, porque en la realidad uno suele realizar la puesta en estación justamente tras realizar alguna modificación en la configuración. Por otra parte, si rotamos la cámara, esto deja de ser cierto e igualmente hay que realizar el proceso completo.
Lo que sí es cierto es que de acuerdo con esta conclusión, podemos comprobar si el margen de error de nuestras medidas y cálculos es muy elevado o no. Para ello hemos comparado las coordenadas de rotación en R.A. que hemos obtenido en todos los casos y hemos podido comprobar que efectivamente son siempre aproximadamente los mismos. El margen de error que hemos detectado entre unos casos y otros es de un máximo de unos ±4 píxels, lo que con nuestra configuración corresponde a unos ±10 arcseg.
En definitiva, todas las medidas y sus cálculos asociados que hemos realizado consideramos que tienen un margen de error de ±10 arcseg, lo que sigue constituyendo una excelente aproximación.
Todos los cálculos se realizaron con el prototipo que creamos en Excel, debido a que en su momento aún no habíamos desarrollado la aplicación SV aligner.